
| Genre: | Compilation Of Arcade Games |
| Publisher: | Database |
| Contents: | |
| See Also: | The programs on this Cassette were supplied in type-in format in the magazine Electron User 4.10. |
| Cover Art Language: | English |
| Machine Compatibility: | Acorn Electron |
| Release: | on Cassette |
| Compatible Emulators: | Elkulator 1.0 (PC (Windows)) |
| Original Release Date: | 1st July 1987 |
| Original Release Price: | Unknown |
| Market Valuation: | £2.50 (How Is This Calculated?) |
| Item Weight: | 64g |
| Box Type: | Cassette Single Plastic Clear |
Variant Items
There are 0 other items featuring this same game (that we know about!). Click any of them for their details.
Active Auctions
Closed Auctions
Auction Price Watch
Worried you're being ripped off? Closing prices on eBay can help you decide what a reasonable price is for a particular item.
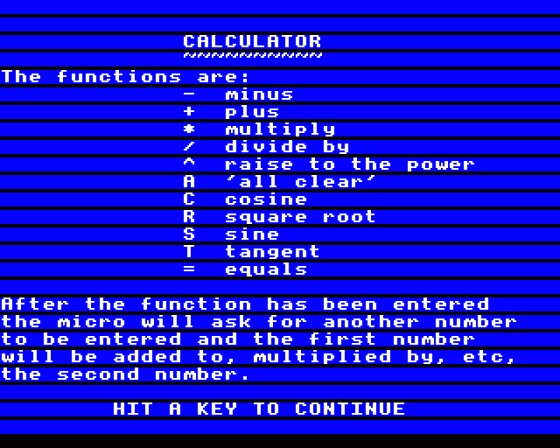
Full Instructions
BIOMORPHS
Mike Cook does his best to improve on nature
 Anyone watching Horizon on BBC2 a couple of months back about Darwinian evolution could not fail to be impressed by the simulated evolution of the little figures known as biomorphs.
Anyone watching Horizon on BBC2 a couple of months back about Darwinian evolution could not fail to be impressed by the simulated evolution of the little figures known as biomorphs.
I was so taken by it that I laid down my soldering iron and started to program my own version for the Electron.
The principles of the simulation are explained in chapter 3 of Richard Dawkins' book "The Blind Watchmaker". He demonstrates that dramatic large scale development of organisms may be achieved by the accumulation of numerous small changes.
The appearance of any creature is determined by its genes which are passed on to its offspring to produce near identical creatures. However, every so often one of the genes mutates or changes slightly resulting in a significantly different creature.
If this creature has a slightly increased chance of survival then it will prosper and an increasing number of the population will carry the same gene pattern. Eventually the whole of the population may contain the same gene types.
In our computer simulation, to save time, each offspring acquires one mutated gene from its parents.
We can then choose the child to breed from for the next generation. This is more like selective breeding that natural selection, but if you equate the ability to please the selector with chances of survival, then it amounts to the same thing.
The small creatures in the simulation, christened biomorphs by Dawkins, are controlled by six genes. In Dawkins' original simulation there were nine, but the display and memory constraints on the Electron necessitate a little simplification.
The basic shape is a simple bifurcating tree drawn by a recursive procedure and each gene controls some aspect of the drawing.
It is not important to understand what the genes do. In fact it could be considered to be an undue influence on your selection. However, the way colour is handled does need a little explanation.
Each biomorph is basically two coloured and at each level of recursion the colour number is incremented by some fraction depending upon a gene value.
At an incremental value of one the colour changes every recursion level so if this increment is small the biomorph might not change colour at all.
Another gene controls the two colours actually displayed on screen.
When this mutates a third colour, selected at random, can be substituted in place of any one of the colours used.
Due to the limitations on the number of colours that can be displayed on a Mode 1 screen, this third mutated colour is also used for drawing the boxes and labelling the biomorphs. The two colours of the biomorph may well map to the same displayed colour, in which caes the create will be of a single colour.
When you run BIOMORPHS you are invited to choose the starting position for your evolution. The choices are a microbe, where all the gene values are set close to the minimum, a random point chosen close to the minimum values or some pre-set point.
Using this last option you can continue breeding from where you left off it you have made a note of the gene values.
| Gene | Function |
| 0 | Depth of recursion used |
| 1 | Basic size of line |
| 2 | Branching angle |
| 3 | Branching angle incremented at each new level of recursion |
| 4 | Colour incremented at each new level of recursion |
| 5 | Displayed colour |
At the centre of the screen is the parent biomorph and in the twelve surrounding boxes are the mutated offspring. Each mutation contains only one gene different from its parent.
There are twelve offspring because each of the six genes can change by a positive or negative increment. Note that they all look very similar - there will only be slight differences between them. In fact, at the smaller sizes these differences might not be discernible.
The gene values are extremely interdependent and all their effects grow with increasing complexity.
You will be invited to choose an offspring from which to breed the next generation and this can be selected by pressing any key from A to L. If any other key is pressed the value of the parent's genes will be printed and the parent will be drawn.
There is nothing in the program to stop the biomorphs growing out of their boxes but this can be prevented by the appropriate selection of offspring to breed form.
Many creatures or shapes can be evolved. One simple one is shown in the screenshot. It is fun to give your creatures names - I call these bumble bees.
You are not restricted to biological shapes, however; you can get a very good likeness to small space invader creatures or space ships.
This is a program that can be extensively tinkered with; the gene maximum, minimum and increments are all contained in data statements and can be easily altered. You could also include a feature to record the progress (gene values of each generation parent) of your creatures on disc file or printer.
In a sense, as Dawkins points out, you are not creating the creatures but discovering them. However, as the number of possible creatures is so large that the two processes become very similar.
The program as printed is capable of generating 120,736,980 shapes which, if you could view them at the rate of one per second, would take you just over 3.8 years to see them all - so get cracking!
MAZEBUGS
MAZEBUGS is a graphic adventure with you cast as chief wizard of the Great Temple in the City of Axon
 Your most prized possession is a chalice of gold with magical powers that is on show in the main hall of the temple.
Your most prized possession is a chalice of gold with magical powers that is on show in the main hall of the temple.
A jealous rival wizard sneaks into the temple to steal the chalice in an effort to depose you.
He hides it in the middle of a maze of lookalike passages. This maze is inhabited by carnivorous mazebugs and these hideous creatures walk the dank corridors gobbling up any adventurer who dares enter.
After many days travel you finally reach the maze. As you enter an invisible barrier is erected barring your exit as the mazebugs advance.
Your only hope of survival is to fight the monstrous creatures, find the chalice and use its magical powers to raise the barrier and return to Axon.
Your adventure starts at the entrance and the upper part of the screen display gives a 3D perspective view of the maze in front of you.
The lower half of the screen is reserved for text and you can enter commands such as GO FORWARD, TURN LEFT and TURN RIGHT.
Although the vocabulary is quite small, the parser is fairly intelligent and will understand complex sentences such as HIT MAZEBUG WITH BEER CAN though it is best to keep them simple.
Each time you move to a new location the display is re-drawn to show your new position.
As you explore the maze you'll find weapons to fight the mazebugs (you can try hitting thwm with your fist if you haven't anything else). Tools, food and drink are also available as well as an old parchment map.
You can discover quite a lot by studing the listing, but it's no use trying to find where the mazebugs or chalice are.
They are all placed in different locations each time you play. This means that unlike other adventures, once you have solved the game you can play it again and it will be completely new. If you wish you can even re-design the maze.
This super adventure will keep you occupied for hours so get cracking and good luck.
NINE MEN'S MORRIS
Arthur Lindon resurrects a 3000-year-old board game
 We used to think that NINE MEN'S MORRIS was a strange dance, performed in country villages to help the crops grow. Now Arthur Lindon with the help of a little history has put us right.
We used to think that NINE MEN'S MORRIS was a strange dance, performed in country villages to help the crops grow. Now Arthur Lindon with the help of a little history has put us right.
NINE MEN'S MORRIS is a game first played more than 3,000 years ago. A stone slab, engraved with the playing board, found in a tomb dating from about 1400 BC, substantiates this.
Like the original, the computer game is for two players, each with nine counters. The first player to move is selected at random by the computer and play begins with opponents placing counters on the vacant points.
The object of the game is to form one or more mills. A mill is a row of three counters of the same colour in a straight line. When this is achieved a player can remove one of the opponent's counters. But the counter removed must not be part of a mill.
In the screenshot, it is red to go and if he places a counter at B a mill will be formed through A-B-C. He can then remove a blue counter - Q or W is best - preventing blue from gaining a mill through Q-T-W on his next turn.
If a player is reduced to two counters or unable to move he loses the game. Play continues when all the counters have been laid out by sliding a counter along a line to an adjacent point, provided that it is vacant. Again the aim is to form a mill.
If a counter in a mill is moved, as may be necessary in normal play, all counters in that mill, unless forming part of another mill, become liable to capture.
It may be necessary to waive the right of removal and to do this press Z. It is the only time a turn may be missed. To yield to your opponent at any time press Y.
For ease of use, the positions of the counters are referred to on the board by letters, but the computer sees them as numbers 1 to 24. Three permanent arrays are set up X(n), Y(n) and Z(n), each array being 25 elements long.
The arrays X(n) and Y(n) hold the actual character positions of the counters in the horizontal and vertical directions, Z(n) holds the numbers of the positions reading the grid from left to right and top to bottom.
For example, the first three numbers in Z(n) are 1, 10 and 22 which correspond to the grid positions A, J and V.
The two other arrays C(n) and M(n) are constantly changing during the game. The C(n) array is set to the colour of the counter occupying position n or zero if vacant and M(n) is set to one if the counter at position n is part of a mill or zero otherwise.
In the early stages counters are played one at a time by each player on vacant points using PROCplace.
When the two stocks are exhausted, selected couonters are moved along the lines to the next point, provided it is vacant, using PROCmove.
After each turn, PROCcheck checks whether a mill has been formed. If it has PROCcapture deals with the removal of the opponent's counter.
It may sometimes be necessary for strategic reasons, to move a counter out of a mill during a game (a counter moved out of a mill and back again reforms the mill). PROCreset scans the grid each move to check for the formation of a new mill.
Screen Designers
The following utilities are also available to allow you to edit the supplied screens of this game:
Cheats
Download
At least one physical version of this item is currently for sale in the shop.
A digital version of this item can be downloaded right here at Everygamegoing (All our downloads are in .zip format).
| Download | What It Contains |
|---|---|
| A digital version of Electron User 4.10 suitable for Elkulator 1.0 (PC (Windows)) | |
| A digital version of Electron User 4.10 suitable for Elkulator 1.0 (PC (Windows)) |
Report A Problem
We thank you from the bottom of our hearts if you report something wrong on our site. It's the only way we can fix any problems!
You are not currently logged in so your report will be anonymous.
Add Note
Release Country
Change the country to update it. Click outside of this pop-up to cancel.
Scan Of Selected Article
If you auction an item, it will no longer show in the regular shop section of the site.